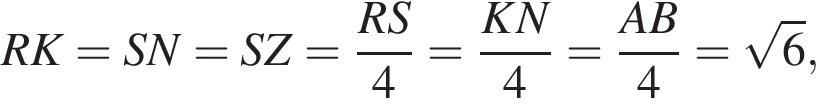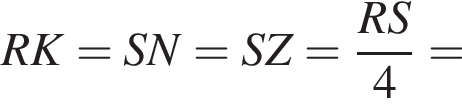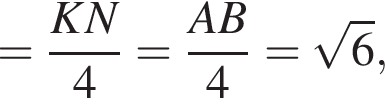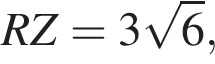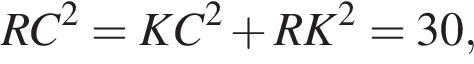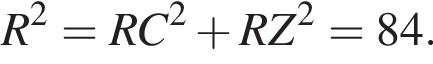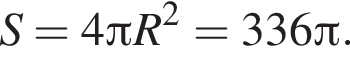Укажите номер точки, которая принадлежит графику функции y = 5x.
Централизованное тестирование по математике, 2020
Если вписанный угол KML изображенный на рисунке, равен 38°, то вписанный угол KNL равен:
Укажите номер выражения для определения натурального числа, содержащего с десятков и 3 единицы (с — цифра).
| 1) c + 3 | 2) 3c | 3) 3c + 10 | 4) 10c + 3 | 5) 30 + c |
Определите, на сколько неизвестное слагаемое меньше суммы, если известно, что x + 20 = 80.
Среди точек С(33), D(24), Е(28), F(43), К(12) координатной прямой укажите точку, симметричную точке А(5) относительно точки В(19).
Найдите значение выражения 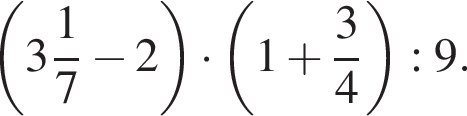
На рисунке изображен треугольник АВС, в котором
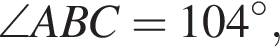
 Используя данные рисунка, найдите градусную меру угла ANM четырехугольника ABMN.
Используя данные рисунка, найдите градусную меру угла ANM четырехугольника ABMN.
У Юры есть некоторое количество марок, а у Яна марок в 2 раза больше, чем у Юры. Мальчики поместили все свои марки в один альбом. Среди чисел 26; 38; 20; 37; 39 выберите то, которое может выражать количество марок, оказавшихся в альбоме.
На координатной плоскости даны точка А, расположенная в узле сетки, и прямая l (см. рис.). Определите координаты точки, симметричной точке А относительно прямой l.
График уравнения 1,8x − 0,6y = a проходит через точку А(−2; 9). Найдите число a.
Из двух пунктов, расстояние между которыми равно S, одновременно навстречу друг другу с постоянными скоростями отправляются по течению реки плот (П) и против течения реки катер (К). На рисунке приведены графики их движения в течение часа с момента отправления. Определите, за сколько минут от начала движения плот придет в пункт, из которого отправился катер.
Внесите множитель под знак корня в выражении 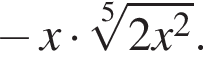
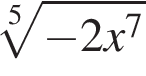
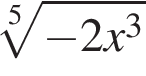
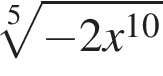
В окружности радиуса 13 проведена хорда АВ. Точка М делит хорду AВ на отрезки длиной 10 и 12. Найдите расстояние от точки М до центра окружности.
Для неравенства (8 − x)(x + 3) ≥ 0 укажите номера верных утверждений.
1) Число 0 не является решением неравенства;
2) неравенство равносильно неравенству 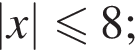
3) количество всех целых решений неравенства равно 12;
4) неравенство верно при x ∈ [−2; 3];
5) решением неравенства является промежуток [−8; 3].
Длины диагоналей ромба являются корнями уравнения 0,1x2 − 2,2x + 7,4 = 0. Найдите площадь ромба.
На одной стороне прямого угла О отмечены две точки А и В так, что ОА = 1,7, OB = а, ОА < ОВ. Составьте формулу, по которой можно вычислить радиус r окружности, проходящей через точки А, В и касающейся другой стороны угла.
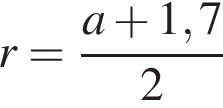
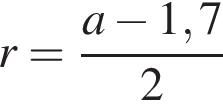
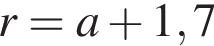
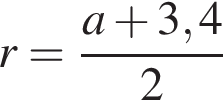
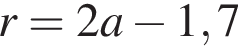
Число А = 5,43 является результатом округления числа В до сотых. Если |А − В| = 5 · 10−3, то число В равно:
Высота цилиндра в 3 раза больше радиуса его основания. Найдите объем цилиндра, если радиус основания равен ![]()
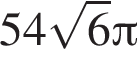

Найдите произведение наименьшего целого решения на количество всех целых решений неравенства 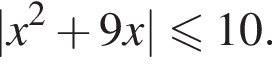
SABCD — правильная четырехугольная пирамида, все ребра которой равны 37. Точка М — середина ребра SA. Точка N ∈ SD, DN : NS = 1 : 3. Найдите длину отрезка, по которому плоскость, проходящая через точки N, М, В, пересекает основание ABCD пирамиды.
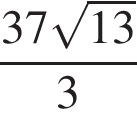
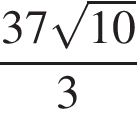
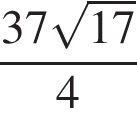
Дана арифметическая прогрессия (аn), у которой а9 − а5 = 12, a10 = 14. Для начала каждого из предложений А−В подберите его окончание 1−6 так, чтобы получилось верное утверждение.
| Начало предложения | Окончание предложения | |
| А) Разность этой прогрессии равна ... Б) Первый член этой прогрессии равен ... В) Сумма первых восьми членов этой прогрессии равна ... | 1) 2 2) −13 3) 4 4) −20 5) 3 |
Ответ запишите в виде сочетания букв и цифр, соблюдая алфавитную последовательность букв левого столбца. Помните, что некоторые данные правого столбца могут использоваться несколько раз или не использоваться вообще. Например: А1Б1В4.
Выберите три верных утверждения, если известно, что  и
и 
1) 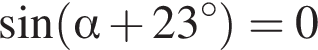
2) 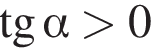
3) 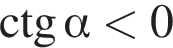
4) ![]() — угол первой четверти
— угол первой четверти
5) 
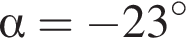
6) 
Ответ запишите в виде последовательности цифр в порядке возрастания. Например: 234.
В каждую из трех корзин положили одинаковое количество яблок. Если в одну из корзин добавить 19 яблок, то в ней их окажется меньше, чем в двух других корзинах вместе. Если же в эту корзину положить еще 23 яблока, то в ней их станет больше, чем было первоначально в трех корзинах вместе. Сколько яблок было в каждой корзине первоначально?
В равнобедренную трапецию, площадь которой равна 115, вписана окружность радиуса 5. Найдите периметр трапеции.
Найдите произведение наименьшего корня (в градусах) на количество различных корней уравнения  на промежутке (−90°; 90°).
на промежутке (−90°; 90°).
Точки N и М лежат на сторонах АВ и AD параллелограмма ABCD так, что AN : NB = 1 : 2, AM : MD = 1 : 2. Площадь треугольника CMN равна 45. Найдите площадь параллелограмма ABCD.
Найдите произведение наибольшего целого отрицательного и наибольшего целого положительного решений неравенства
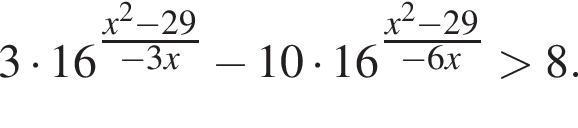
Найдите произведение корней (корень, если он единственный) уравнения 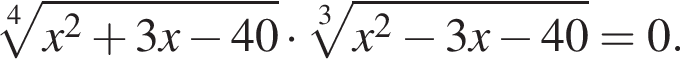
ABCA1B1C1 — правильная треугольная призма, у которой AB = 5, AA1 = 5. Точки Р и Q — середины ребер АВ и А1С1 соответственно. Найдите значение выражения 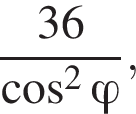 где
где ![]() — угол между прямыми PQ и АВ1.
— угол между прямыми PQ и АВ1.
Найдите сумму квадратов корней (корень, если он единственный) уравнения 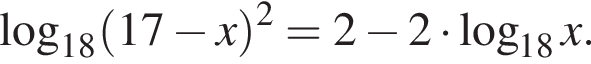
Найдите все пары (m, n) целых чисел, которые связаны соотношением m2 + 2m = n2 + 6n + 13. Пусть k — количество таких пар, m0 — наименьшее из значений m, тогда значение выражения k · m0 равно ... .
ABCDA1B1C1D1 — куб, длина ребра которого равна ![]() Сфера проходит через его вершины В и D1 и середины ребер BB1 и CC1. Найдите площадь сферы S, в ответ запишите значение выражения
Сфера проходит через его вершины В и D1 и середины ребер BB1 и CC1. Найдите площадь сферы S, в ответ запишите значение выражения ![]()

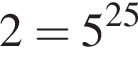 — неверно,
— неверно, — неверно,
— неверно, — неверно,
— неверно, — верно,
— верно,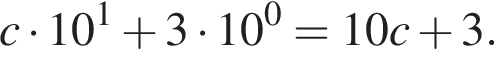
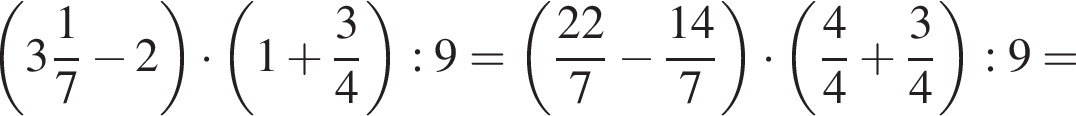
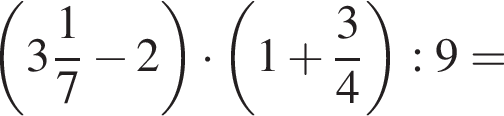
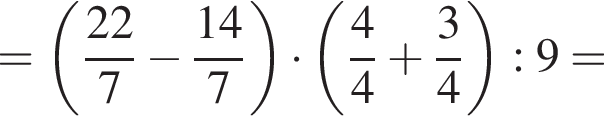
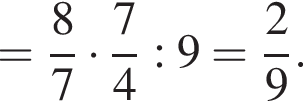
 Так как сумма углов треугольника равна 180°,
Так как сумма углов треугольника равна 180°, 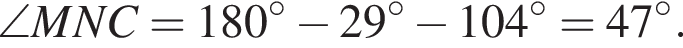 Угол ANM вертикальный с найденным. Значит, он равен
Угол ANM вертикальный с найденным. Значит, он равен 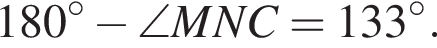
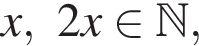 общее число марок 3x должно быть кратно 3. Ясно, что из предложенного числа марок подходит только число 39.
общее число марок 3x должно быть кратно 3. Ясно, что из предложенного числа марок подходит только число 39.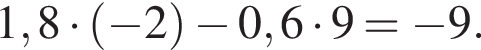
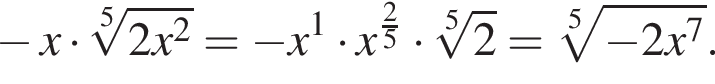
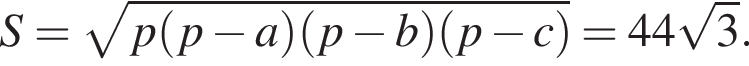
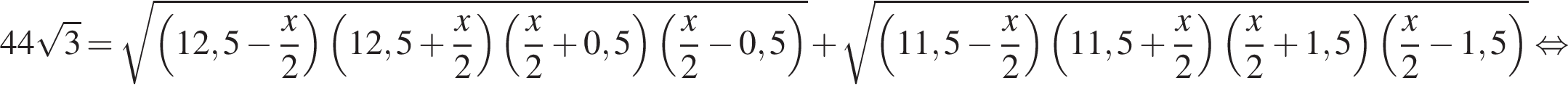

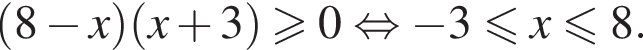
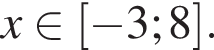 Таким образом, верные утверждения указаны под номерами 3 и 4.
Таким образом, верные утверждения указаны под номерами 3 и 4.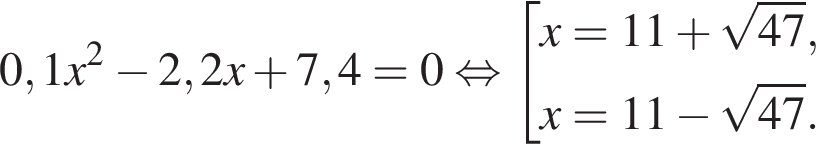
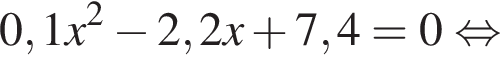
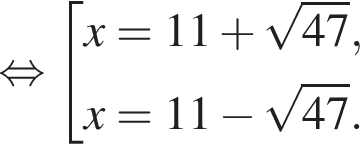
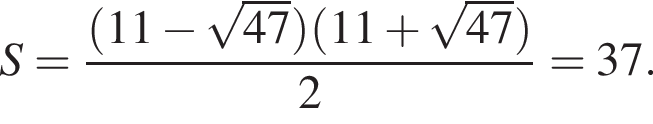
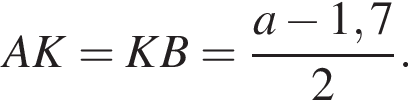
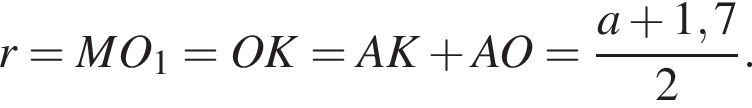
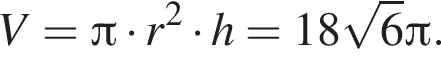
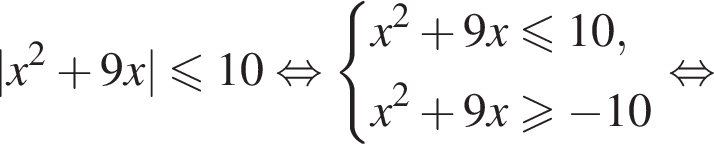
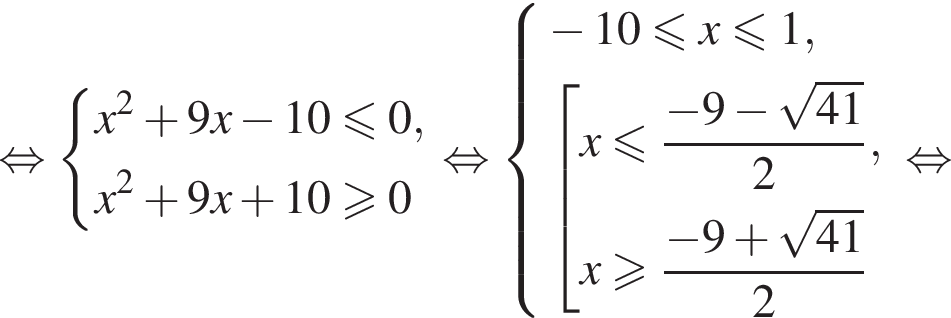
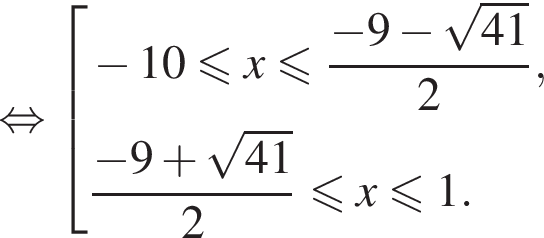
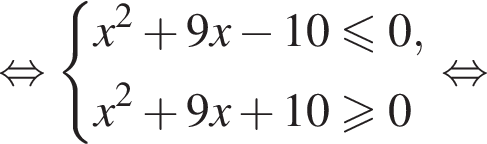
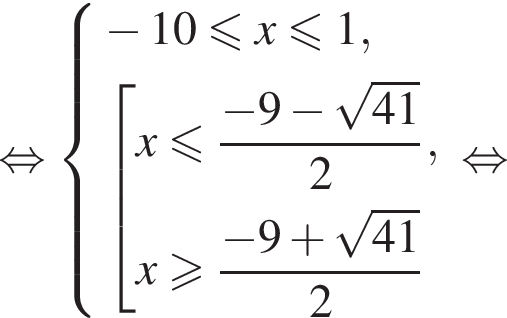
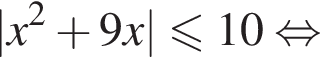
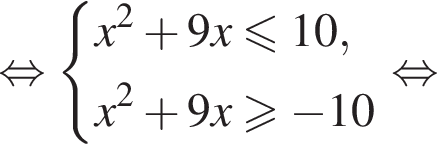
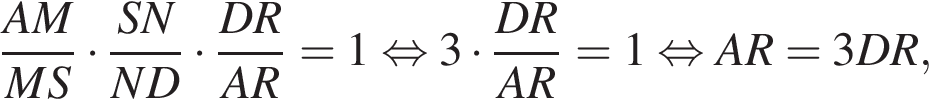

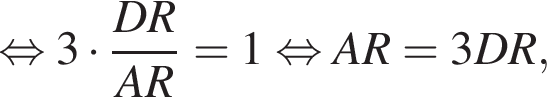
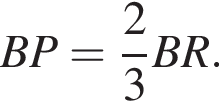 Поскольку
Поскольку 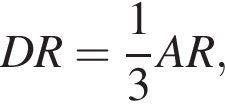 получаем, что
получаем, что 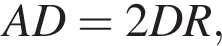
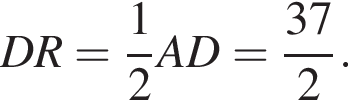 Тогда
Тогда 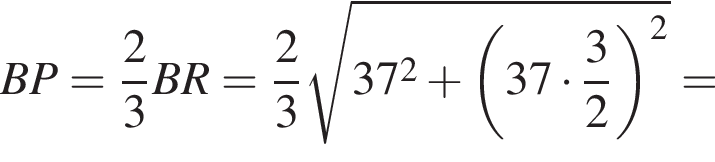
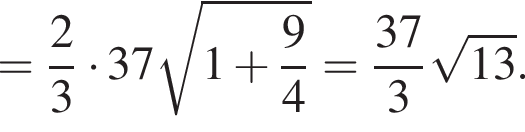
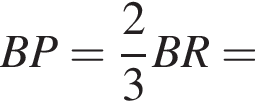
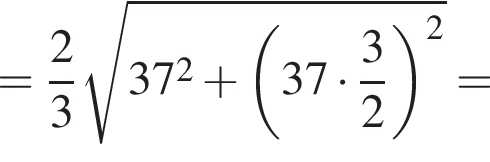
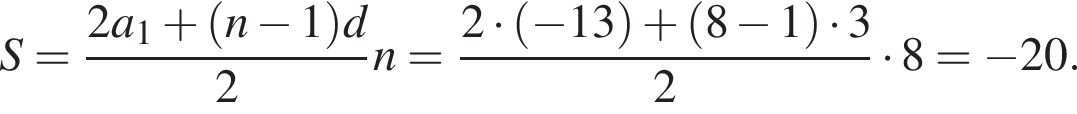
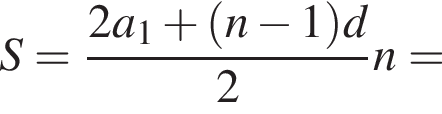
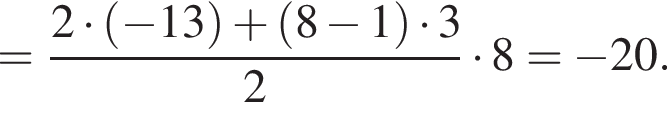
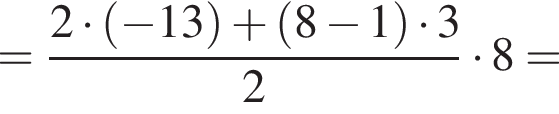
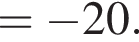
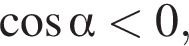 а
а 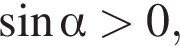 то
то 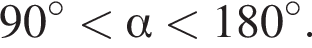 Заметим, что
Заметим, что 
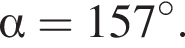 Тогда
Тогда 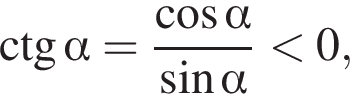 так как
так как 
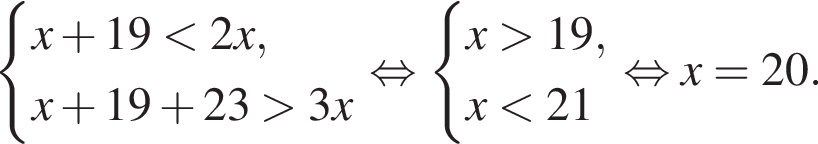
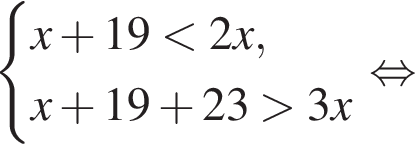
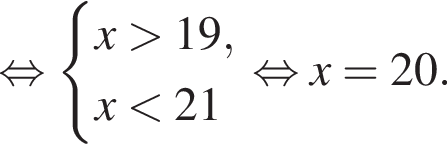
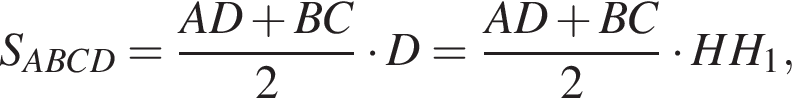 откуда получим:
откуда получим: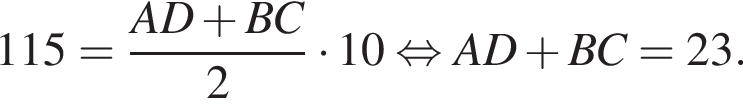
 следовательно, имеем:
следовательно, имеем:
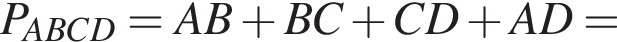
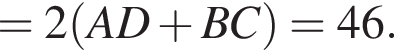


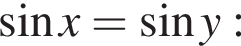
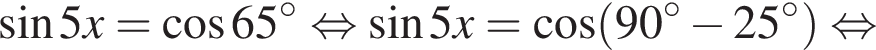
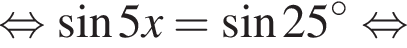
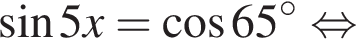

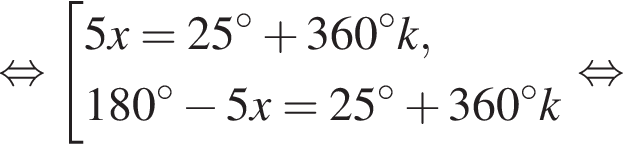
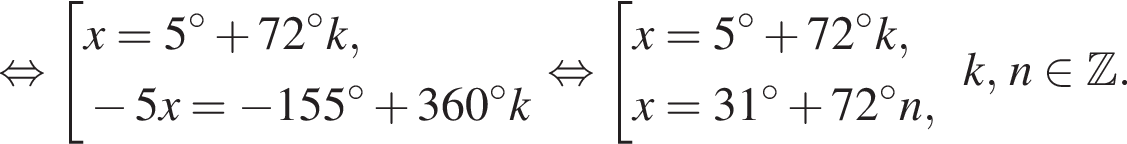
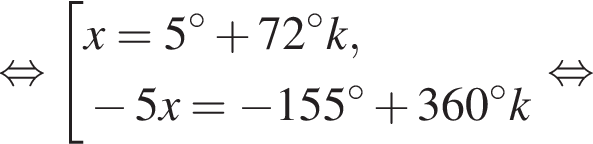
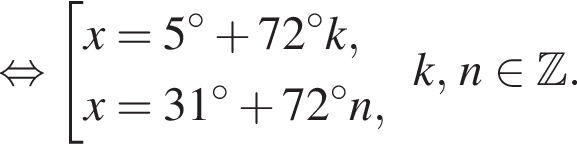

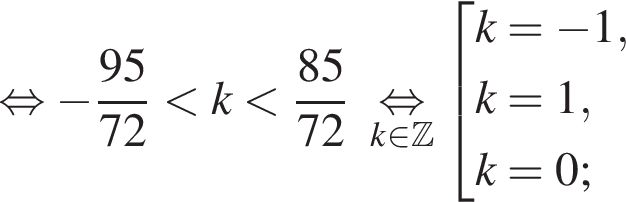


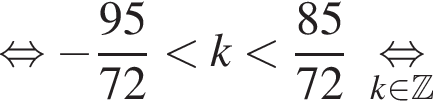
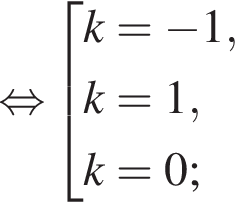

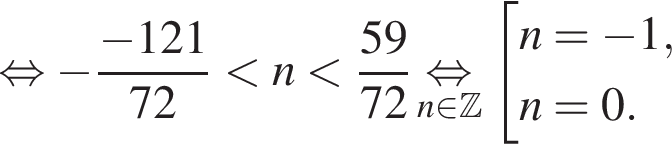
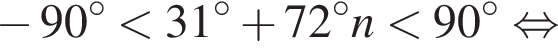

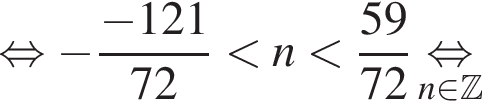
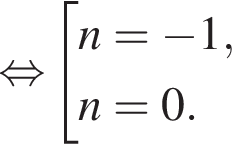
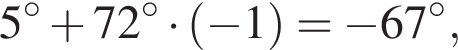
 и
и 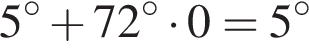 из первой серии и корни
из первой серии и корни  и
и 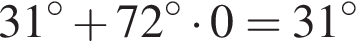 из второй. Наименьший из корней равен
из второй. Наименьший из корней равен 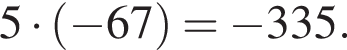
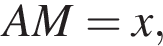 тогда
тогда 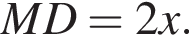 Аналогично
Аналогично 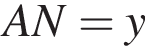 и
и  Площадь параллелограмма представим в виде суммы площадей треугольников, из которых он составлен:
Площадь параллелограмма представим в виде суммы площадей треугольников, из которых он составлен:

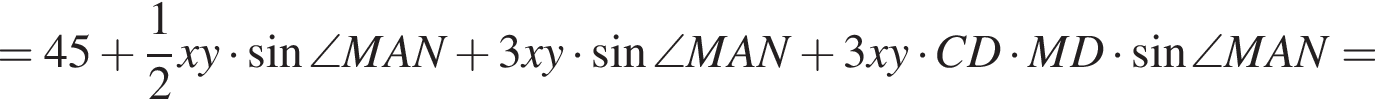
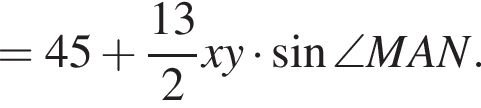
 так как
так как 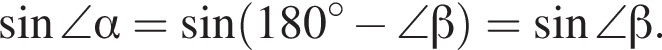 Площадь параллелограмма равна
Площадь параллелограмма равна 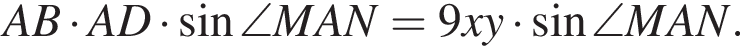 Имеем:
Имеем: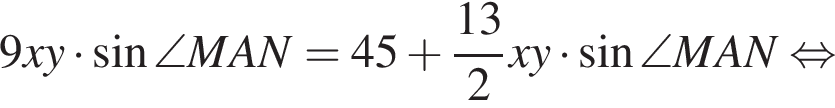
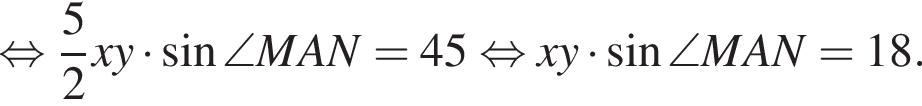
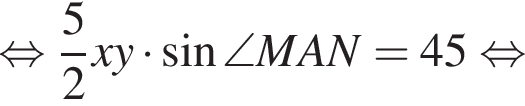

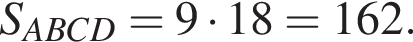
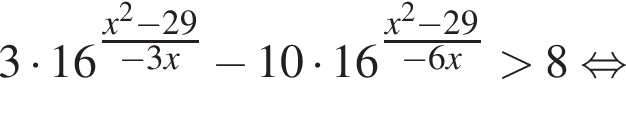
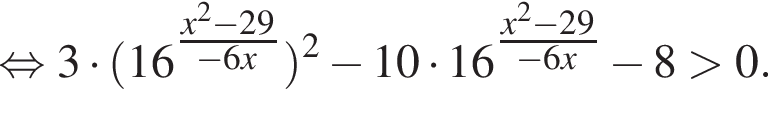
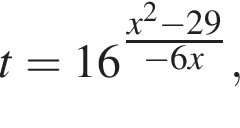 тогда имеем:
тогда имеем: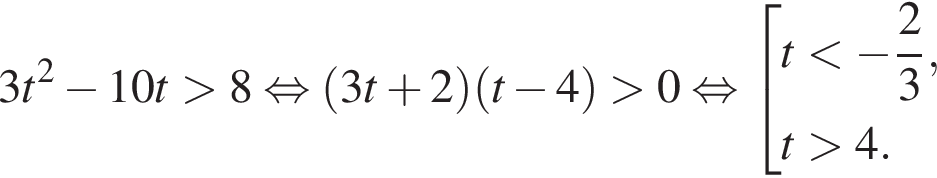
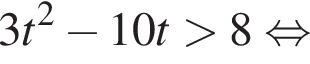
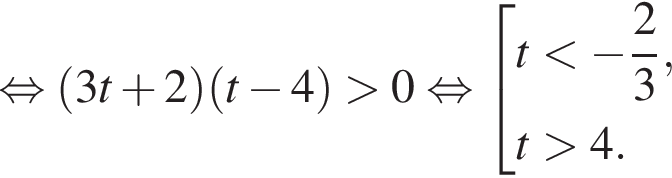
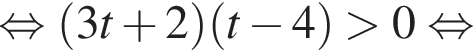
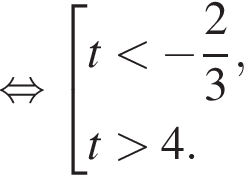
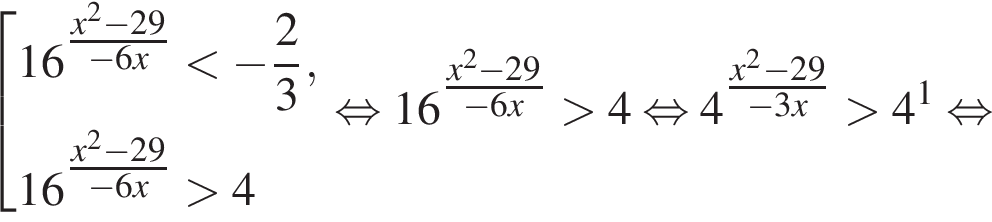
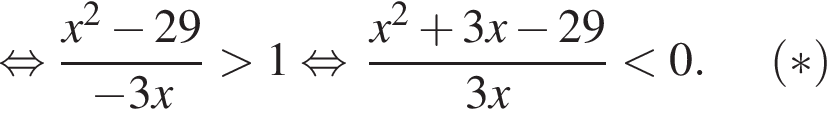
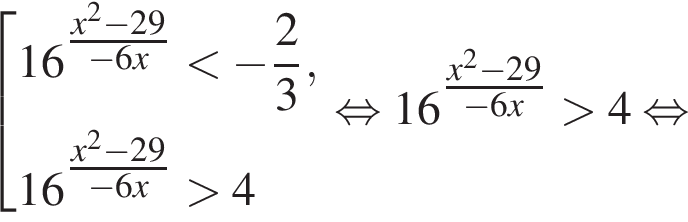
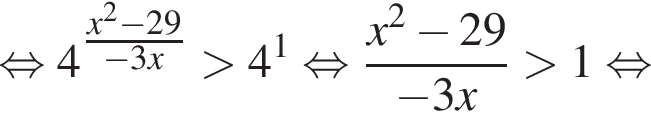
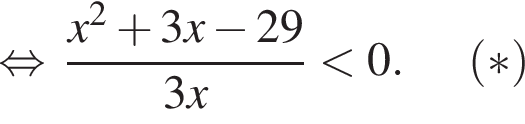
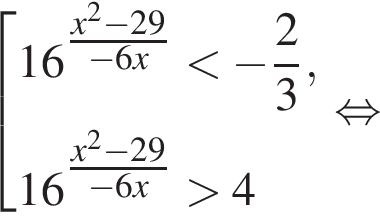
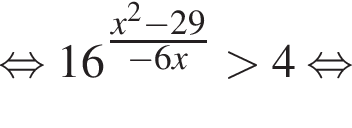
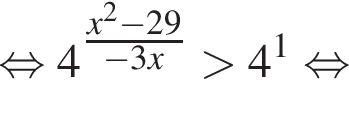
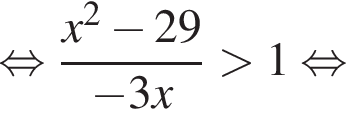
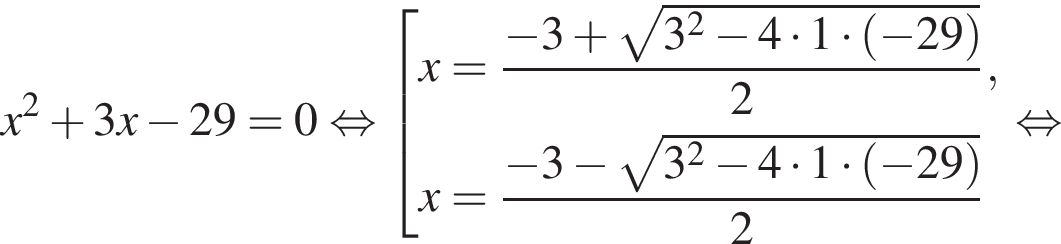
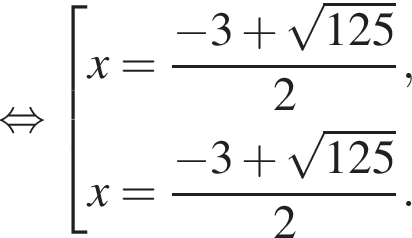
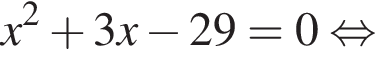
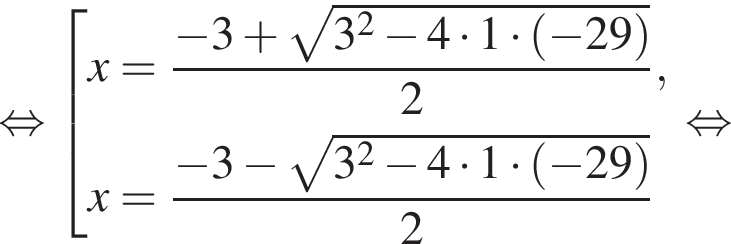
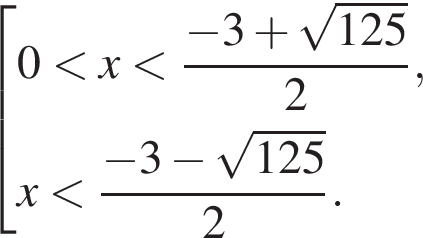
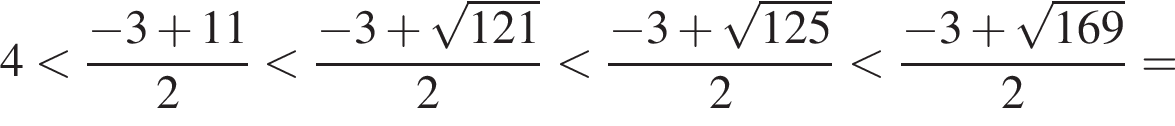
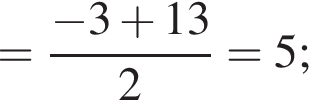
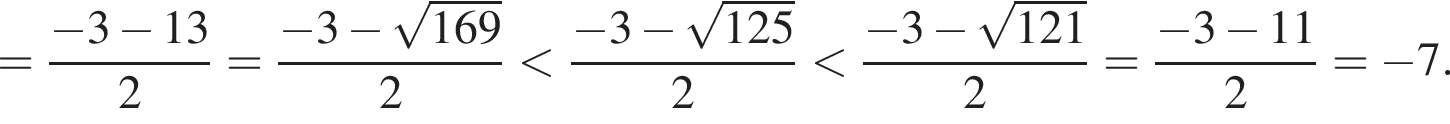
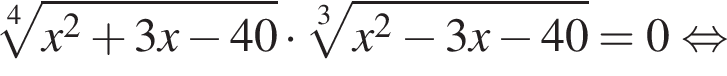
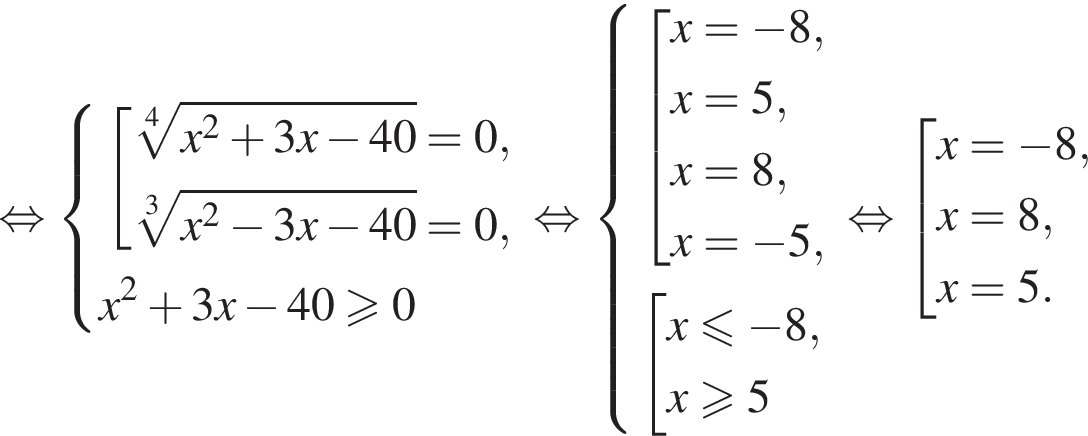
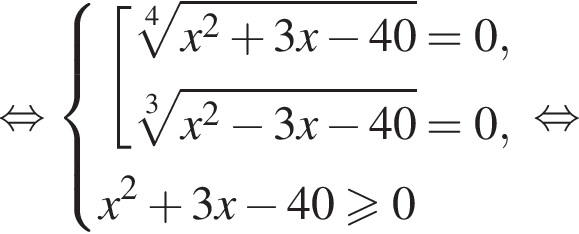
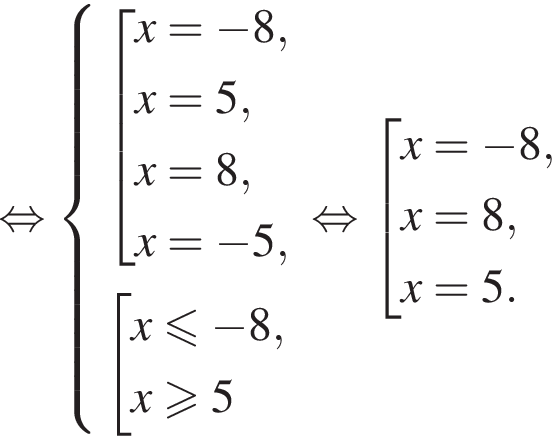
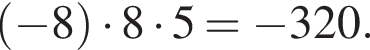
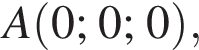
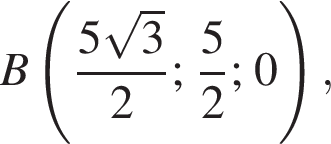
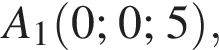
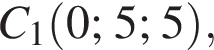 откуда
откуда 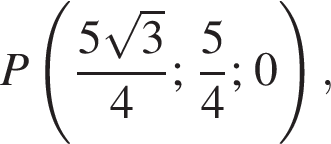
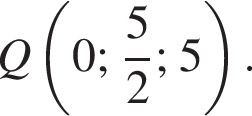 Следовательно,
Следовательно, 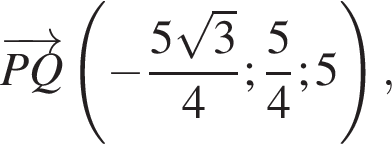
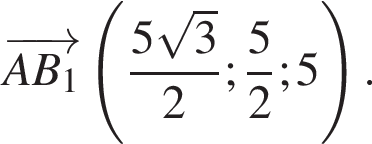
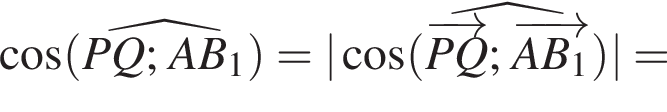
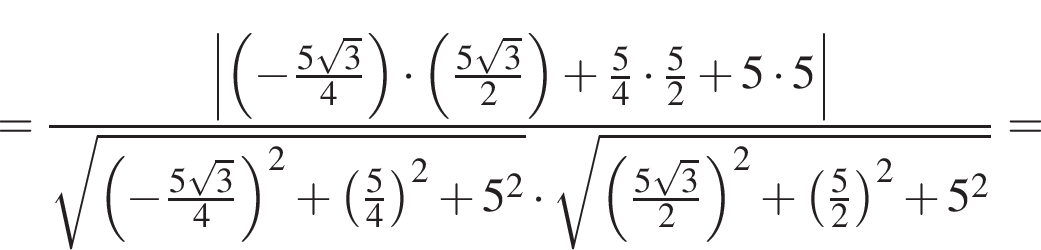
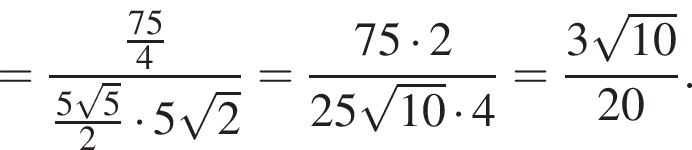
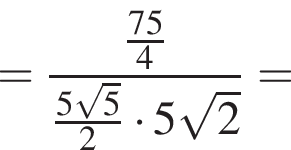
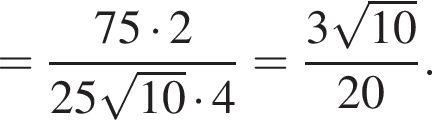
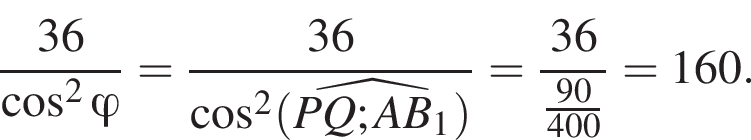
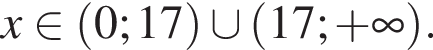 На этой области произведем преобразования:
На этой области произведем преобразования: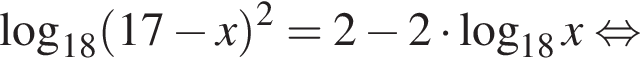
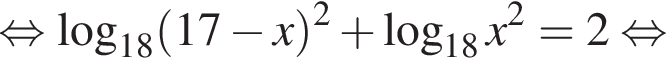
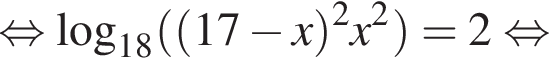

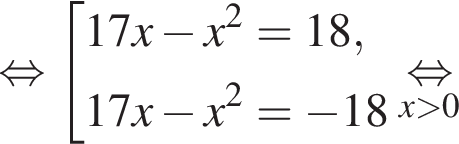
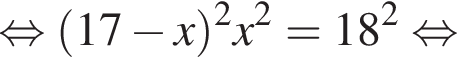
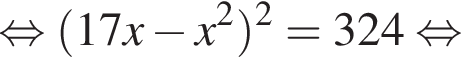
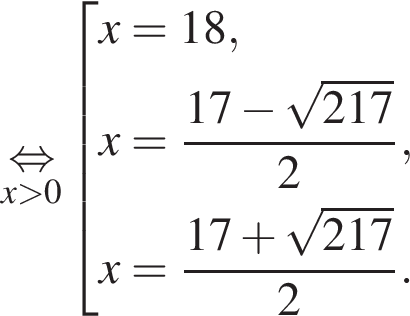
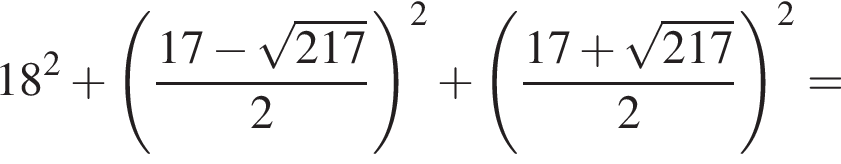
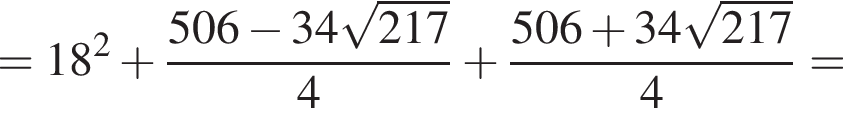

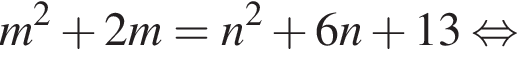
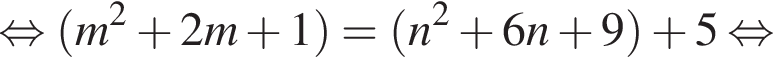
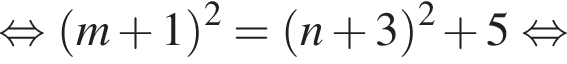

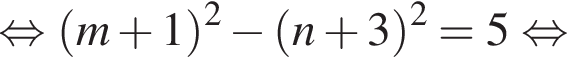

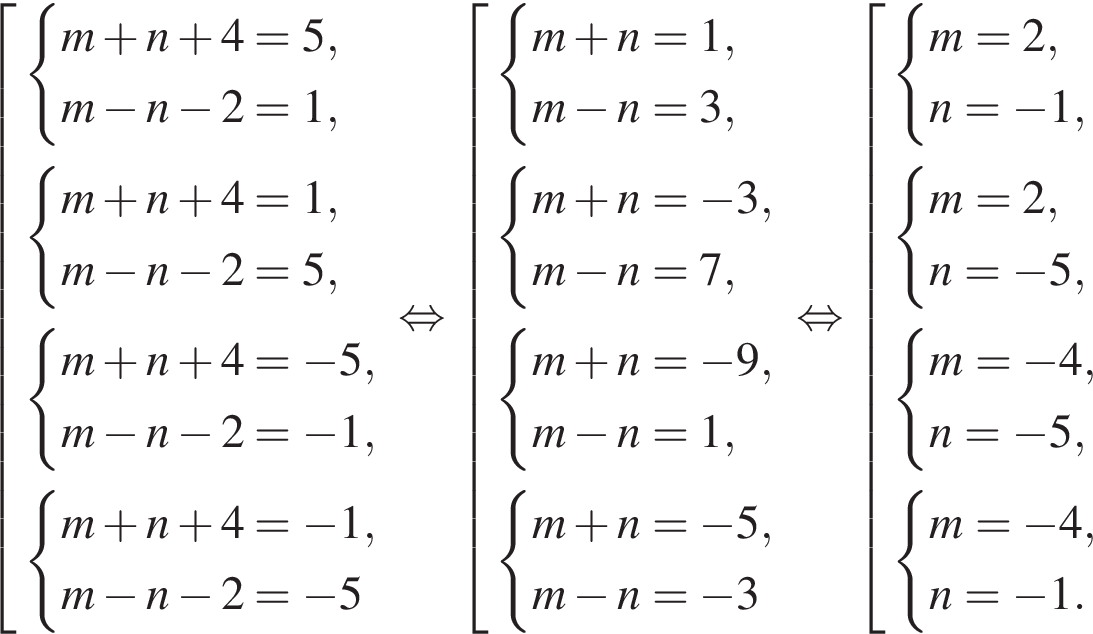
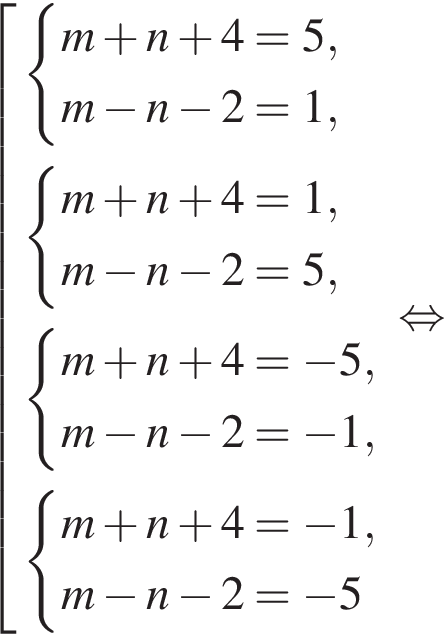
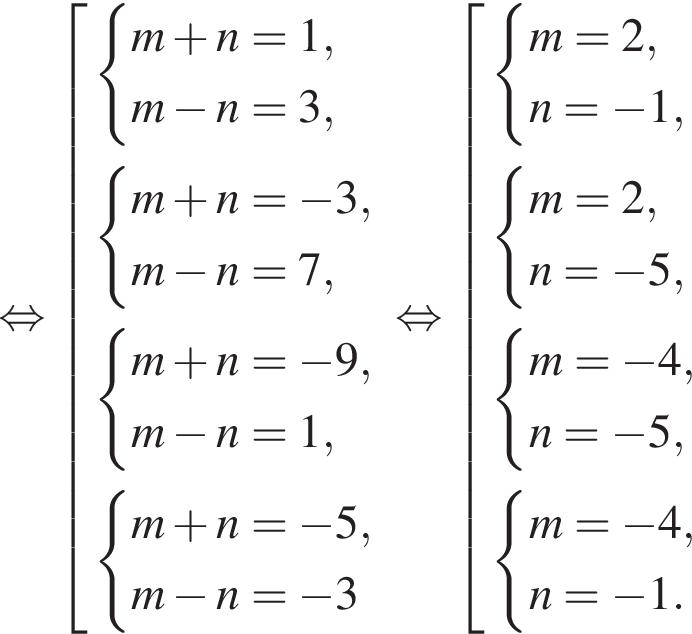
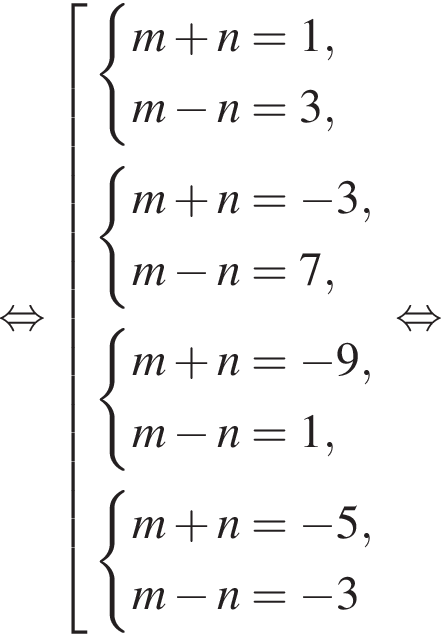
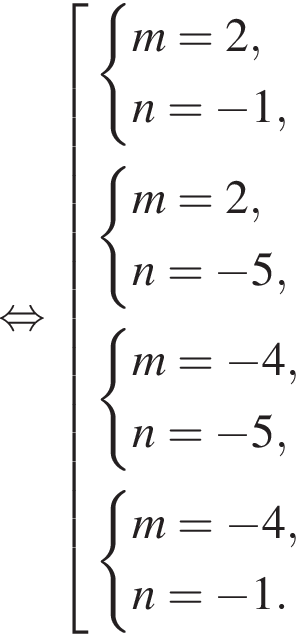
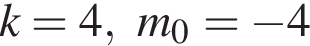 и
и